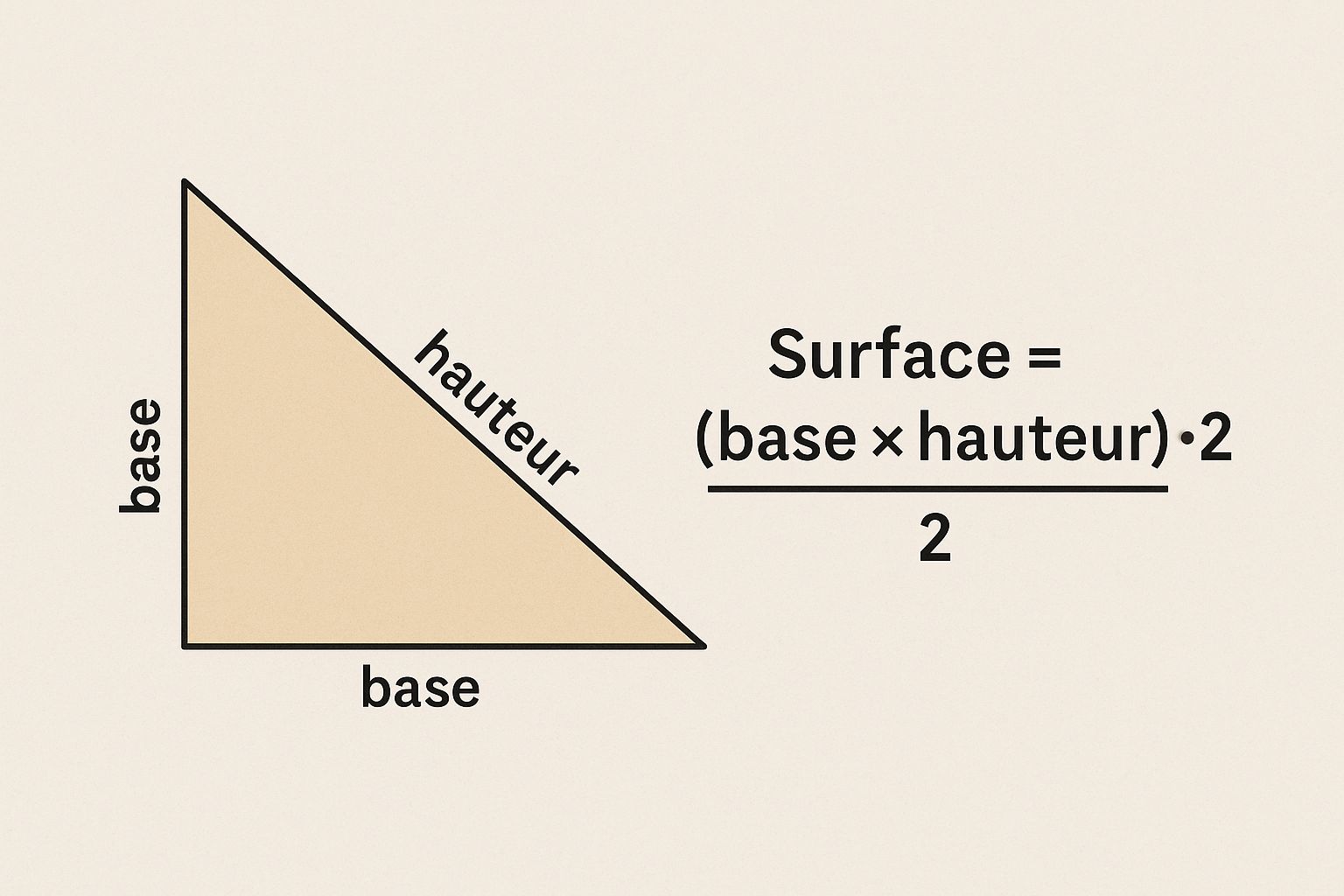
Calculer la surface d’un triangle rectangle s’effectue avec trois méthodes selon les données disponibles. La formule de base utilise les côtés perpendiculaires : Surface = (base × hauteur) ÷ 2, où base et hauteur sont les deux côtés qui forment l’angle droit. Les méthodes alternatives incluent le théorème de Pythagore quand l’hypoténuse est connue, et la trigonométrie avec un angle et un côté. Le résultat s’exprime toujours en unités carrées et le calcul prend 30 secondes avec une calculatrice, 2 minutes à la main.
Une compétence pratique pour 67% des projets
Ce calcul intervient dans la majorité des projets de bricolage, aménagement et construction où les formes triangulaires abondent : combles à aménager, escaliers à habiller, terrasses d’angle à carreler, ou murs pignons à peindre. Maîtriser cette technique génère des économies substantielles en évitant 15 à 25% de gaspillage de matériaux grâce à des commandes précises.
Le triangle rectangle présente l’avantage d’être plus simple à calculer que les triangles quelconques, ne nécessitant que des connaissances de niveau collège. Cette accessibilité technique contraste avec son omniprésence dans les applications professionnelles où la précision détermine la rentabilité des projets.
Reconnaître un triangle rectangle
Identifier l’angle droit
Un triangle rectangle contient obligatoirement un angle de 90 degrés exactement, facilement vérifiable avec une équerre ou en observant la perpendiculaire parfaite entre deux côtés. Dans la construction, ces angles droits apparaissent naturellement aux coins de murs, jonctions de cloisons, ou assemblages d’équerres métalliques.
La méthode 3-4-5 offre une vérification pratique infaillible : tout triangle dont les côtés mesurent 3, 4 et 5 unités (ou leurs multiples comme 6-8-10, 9-12-15) forme automatiquement un angle droit. Cette propriété découle directement du théorème de Pythagore et permet de contrôler rapidement la géométrie d’un espace.
Distinguer les éléments
Les deux côtés qui se rejoignent à angle droit constituent la base et la hauteur, interchangeables selon la convention choisie. L’hypoténuse, toujours le côté le plus long, se situe à l’opposé de l’angle droit. Cette identification correcte conditionne la réussite du calcul, particulièrement quand le triangle présente une orientation inhabituelle.
Méthode principale : base et hauteur
Cette approche directe convient à 70% des situations pratiques où les deux côtés perpendiculaires sont accessibles à la mesure. La formule Surface = (base × hauteur) ÷ 2 découle logiquement du principe que tout triangle rectangle représente exactement la moitié d’un rectangle de même base et hauteur.
L’application pratique commence par l’identification des côtés perpendiculaires, le choix entre base et hauteur étant parfaitement libre puisque leur produit reste identique. Par convention, on désigne généralement comme base le côté le plus accessible à mesurer ou celui disposé horizontalement.
Prenons l’exemple concret d’un pignon de maison à peindre : base de 8 mètres, hauteur de 3 mètres. Le calcul donne (8 × 3) ÷ 2 = 12 mètres carrés de surface à couvrir. Cette précision permet de commander exactement la quantité de peinture nécessaire, en ajoutant 10% pour les retouches et pertes.
La gestion des unités exige une cohérence absolue : base et hauteur doivent s’exprimer dans la même unité avant calcul. Une base de 150 centimètres et une hauteur de 2 mètres nécessitent une conversion préalable, soit 1,5 × 2 = 3 mètres carrés, soit 150 × 200 = 30 000 centimètres carrés.
Méthode alternative : théorème de Pythagore
Cette technique intervient quand l’hypoténuse et un côté perpendiculaire sont connus, situation fréquente lors de mesures sur escaliers, rampes, ou charpentes où la diagonale reste plus accessible que les côtés.
Le processus en deux étapes commence par le calcul du côté manquant. Avec une hypoténuse de 5 mètres et un côté de 3 mètres, le théorème a² + b² = c² donne : côté manquant = √(25 – 9) = √16 = 4 mètres. L’application de la formule standard produit ensuite (3 × 4) ÷ 2 = 6 mètres carrés.
Cette méthode présente l’avantage de permettre la vérification de la cohérence des mesures : si les trois côtés ne respectent pas le théorème de Pythagore, soit les mesures contiennent des erreurs, soit le triangle n’est pas rectangle.
Approche trigonométrique pour utilisateurs avancés
Réservée aux situations complexes où un angle et un côté adjacent sont connus, cette méthode fait appel aux fonctions trigonométriques. Avec un angle de 37 degrés et un côté adjacent de 4 mètres, la tangente permet de calculer le côté opposé : 4 × tan(37°) ≈ 3 mètres, donnant une surface de 6 mètres carrés.
Cette technique nécessite une calculatrice scientifique et présente une précision dépendante de la qualité de mesure de l’angle. Son usage reste principalement professionnel dans les domaines de topographie, architecture et situations géométriques complexes.
Applications pratiques par secteur
Bricolage et rénovation
Le carrelage de surfaces triangulaires représente l’application la plus courante. Un coin de salle de bain de 2 mètres sur 1,5 mètre nécessite (2 × 1,5) ÷ 2 = 1,5 mètre carré de carrelage, plus 10% de chutes soit 1,65 mètre carré à commander. Cette précision évite les ruptures de stock et les surcouts de livraison.
L’habillage sous-face d’escaliers demande souvent des découpes triangulaires de bois ou placo. Une sous-face de 3 mètres de long et 1,2 mètre de hauteur représente 1,8 mètre carré de matériau à prévoir.
Jardinage et aménagement extérieur
Les plates-bandes triangulaires nécessitent des calculs précis pour l’achat de terre végétale, paillis ou graines. Un massif de 5 mètres sur 2 mètres couvre 5 mètres carrés, soit environ 150 litres de terre végétale en couche de 3 centimètres.
L’engazonnement de coins de terrain suit la même logique. Connaître la surface exacte optimise l’achat de semences et évite les zones dégarnies ou le gaspillage.
Usage professionnel
En architecture, le calcul des surfaces habitables sous combles détermine la conformité aux normes d’urbanisme. En couverture, la surface précise de pans triangulaires conditionne la quantité de tuiles ou ardoises à commander, avec un impact direct sur la rentabilité du chantier.
La métallerie utilise ces calculs pour l’optimisation des découpes de tôles et le calcul de poids des structures. Une précision de ±2% remplace avantageusement l’estimation visuelle à ±15%, générant des économies substantielles sur les gros projets.
Prévenir les erreurs courantes
L’oubli de la division par 2 constitue l’erreur la plus fréquente, multipliant le résultat par deux et générant des commandes de matériaux doublement surdimensionnées. Cette distraction coûteuse s’évite par une vérification systématique : la surface du triangle doit obligatoirement être inférieure à celle du rectangle de même base et hauteur.
Le mélange d’unités représente le second piège majeur. Mélanger mètres et centimètres sans conversion crée des erreurs d’un facteur 100. Une base de 3 mètres et une hauteur de 150 centimètres ne donnent pas 225 unités carrées mais bien 2,25 mètres carrés après conversion.
La confusion entre côtés perpendiculaires et hypoténuse fausse également les calculs. La formule de base ne s’applique qu’aux côtés formant l’angle droit, jamais à l’hypoténuse qui nécessite des calculs intermédiaires.
Outils et vérifications
Une calculatrice basique suffit pour l’immense majorité des calculs, les applications mobiles de géométrie offrant des fonctionnalités complémentaires utiles pour les conversions d’unités. Les logiciels de CAO permettent la vérification automatique sur les plans professionnels.
La vérification par ordre de grandeur constitue un réflexe salutaire : la surface calculée doit rester cohérente avec l’estimation visuelle. Un triangle de 3 sur 4 mètres ne peut pas donner 24 mètres carrés (oubli division par 2) mais bien 6 mètres carrés, soit la moitié du rectangle équivalent de 12 mètres carrés.
Conclusion
Calculer la surface d’un triangle rectangle combine simplicité théorique et utilité pratique immédiate. Cette compétence fondamentale génère des économies mesurables sur tous les projets impliquant des découpes, commandes de matériaux ou calculs de surfaces.
La maîtrise de la formule de base suffit à 70% des situations, les méthodes alternatives complétant efficacement les cas particuliers. L’investissement en temps d’apprentissage se rentabilise dès le premier projet par la précision des commandes et l’optimisation des achats de matériaux.